项目与服务

一、项目介绍

本项目针对工业设计中电磁场、声场仿真、地需反演和医学成像等频域波问题，研发基于区域分解的超大规模稀疏代数系统的求解器，研发内容包括迭代算法稳健性分析、及高性能程序包研发。项目旨在提高迭代法收敛速度、克服内瓶颈，并开发计算时间为O(k)的核心求解器模块。

二、项目研究重点

设计并在数学上分析用于在计算机上模拟波传播的新的快速计算方法。特别的，我们考虑频域上基础波方程(例如亥姆霍兹方程、麦克斯韦方程)在复杂传播区域和复杂传播媒介离散系统的求解，采用区域分解法使用若干个小规模的子问题构造全局问题的预条件子来提高Krylov迭代法收敛速度。并将基于轻量级软件平台开发出可供广泛研究人员使用的频域波方程求解算法包。

三、主要产出

学术上，完善区域分解求解器算法在更一般情形下的理论分析，给出算法收敛性和稳定性的证明，指导程序开发和测试。

应用上，基于理论成果开发基于区域分解法的频域波方程求解算法包，开发高度并行的O(k)求解器并整合到轻量级科学计算框架供广泛研究人员使用。

四、具体应用场景及作用

1. 频域波方程的高效稳健求解器可应用于医学成像、大规模天线阵列、微型芯片电磁场和地质勘探等问题的数值仿真，加快数值仿真和工业产品设计的研发周期。

2. 目前研究进入了TRL1理论级，研究团队研发了任意维棋盘式的针对亥姆霍兹方程的区域分解法求解器，解决了超高频问题求解器的收敛性问题，这是世界上第一个针对变波速超高频问题的原创性成果，拉近了频域波问是的理论估计与算法实际性能的差距。

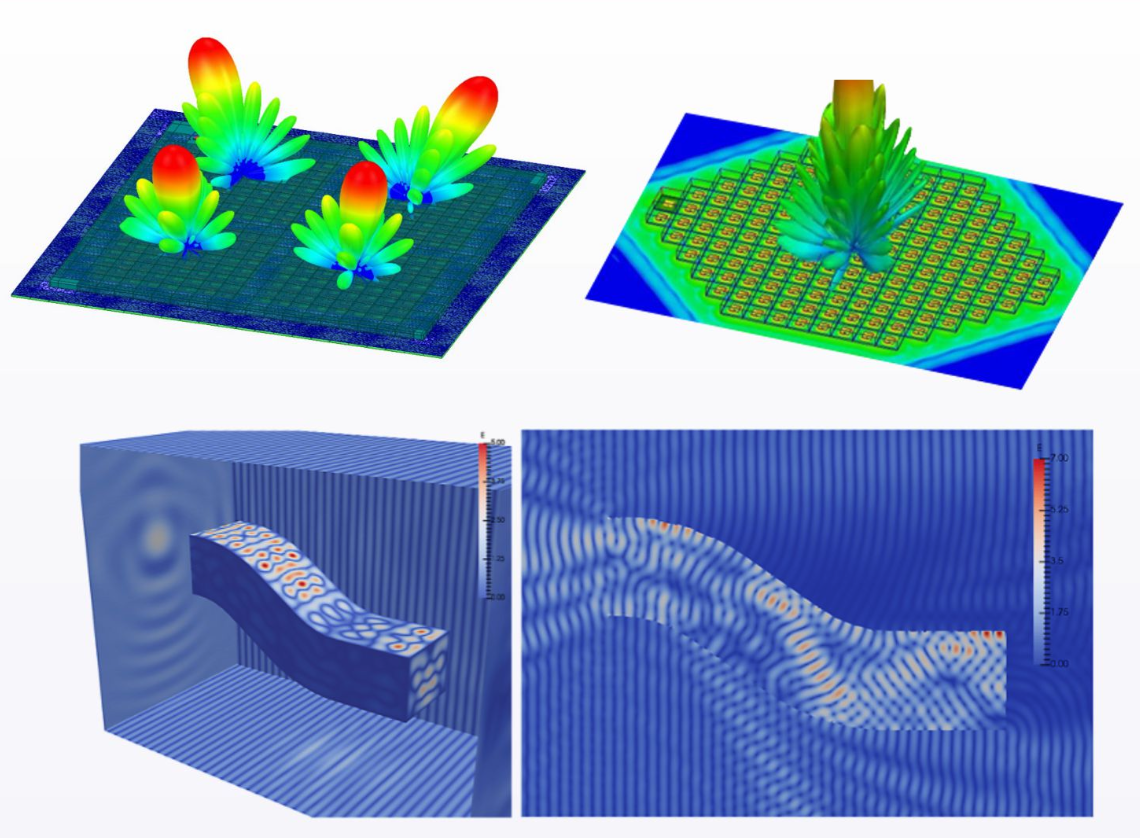
图片来自， Bonazzoli, M., Dolean, V., Graham, I., Spence, E., & Tournier, P. H. (2019). Domain decomposition preconditioning for the high-frequency time-harmonic Maxwell equations with absorption. Mathematics of Computation, 88(320), 2559-2604.

五、合作成果

华为横向项目等