项目与服务

Project Introduction

This project focuses on developing a solver for frequency domain wave problems encountered in industrial design, such as electromagnetic field simulations, acoustic field simulations, geophysical inversion, and medical imaging. It involves the creation of a solver based on domain decomposition for ultra-large-scale sparse algebraic systems, with research content including robustness analysis of iterative algorithms and the development of high-performance software packages. The project aims to improve the convergence speed of iterative methods, overcome internal bottlenecks, and develop a core solver module with a computational time of \( O(k) \).

Research Focus

The project designs and mathematically analyzes new fast computational methods for simulating wave propagation on computers. Specifically, we consider the solution of fundamental wave equations (e.g., the Helmholtz equation, Maxwell's equations) in complex propagation regions and media discrete systems in the frequency domain. By using domain decomposition, we construct preconditioners for the global problem from several smaller subproblems to enhance the convergence speed of Krylov iterative methods. Additionally, we aim to develop a frequency domain wave equation solver package on a lightweight software platform for widespread use by researchers.

Main Outputs

- Academic Contributions: Provide a comprehensive theoretical analysis of the domain decomposition solver algorithms under more general conditions, including proofs of algorithm convergence and stability, to guide software development and testing.

- Practical Applications: Develop a frequency domain wave equation solver package based on theoretical results, create a highly parallel \( O(k) \) solver, and integrate it into a lightweight scientific computing framework for widespread researcher use.

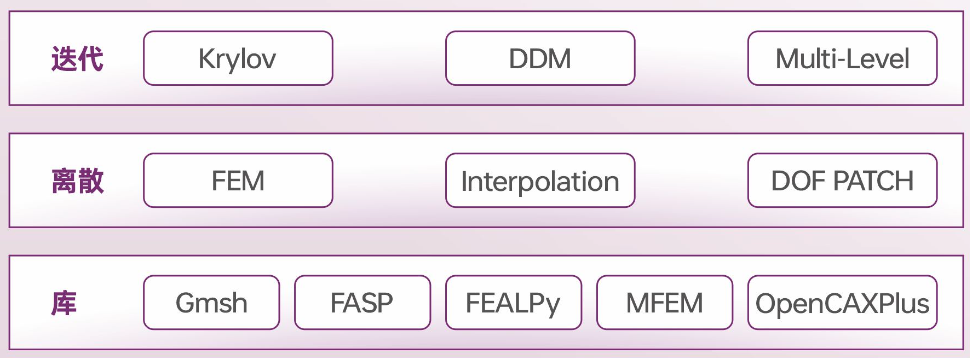
Specific Application Scenarios and Functions

1. The efficient and robust solver for frequency domain wave equations can be applied to numerical simulations in medical imaging, large-scale antenna arrays, electromagnetic fields in microchips, and geological exploration, thereby accelerating the research and development cycle for numerical simulations and industrial product design.

2. The current research has reached TRL1 (theoretical level), and the research team has developed a checkerboard domain decomposition solver for the Helmholtz equation in arbitrary dimensions, addressing convergence issues for ultra-high-frequency solvers. This represents the world's first original achievement for variable wave speed ultra-high-frequency problems, bridging the gap between theoretical estimates and actual algorithm performance.

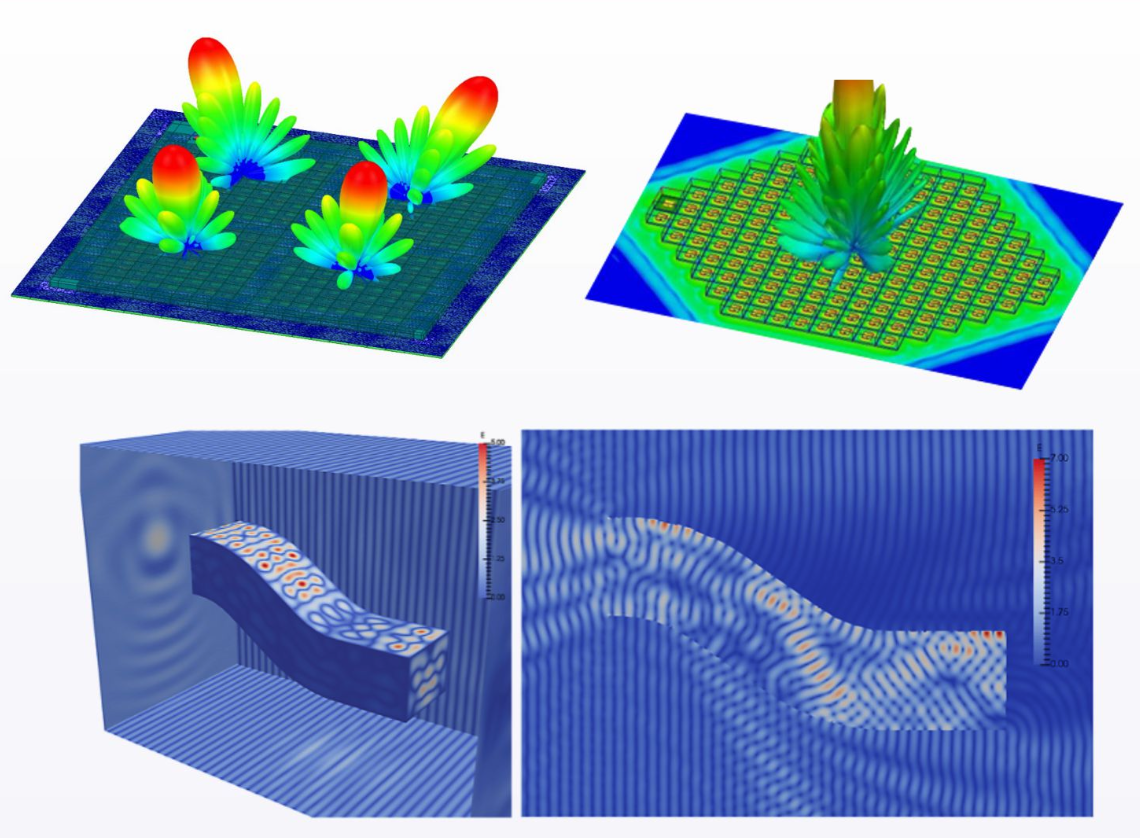
Bonazzoli, M., Dolean, V., Graham, I., Spence, E., & Tournier, P. H. (2019). Domain decomposition preconditioning for the high-frequency time-harmonic Maxwell equations with absorption. Mathematics of Computation, 88(320), 2559-2604.

Collaboration Outcomes

Collaboration with projects such as Huawei's horizontal project, among others.